Recent

Publications

Xu, Y., Horn, S. & Aurnou, J.M.

Transition from wall modes to multimodality in liquid gallium magnetoconvection

https://doi.org/10.1103/PhysRevFluids.8.103503

Coupled laboratory-numerical experiments of Rayleigh-Bénard convection in liquid gallium subject to a vertical magnetic field are presented. The experiments are carried out in two cylindrical containers with diameter-to-height aspect ratio Γ=1.0 and 2.0 at varying thermal forcing (Rayleigh numbers 10⁵≲Ra≲10⁸) and magnetic field strength (Chandrasekhar numbers 0≲Ch≲3×10⁵). Laboratory measurements and numerical simulations confirm that magnetoconvection in our finite cylindrical tanks onsets via nondrifting wall-attached modes, in good agreement with asymptotic predictions for a semi-infinite domain. With increasing supercriticality, the experimental and numerical thermal measurements and the numerical velocity data reveal transitions between wall mode states with different azimuthal mode numbers and between wall-dominated convection to wall and interior multimodality. These transitions are also reflected in the heat transfer data, which combined with previous studies connect onset to supercritical turbulent behaviors in liquid metal magnetoconvection over a large parameter space. The gross heat transfer behaviors between magnetoconvection and rotating convection in liquid metals are compared and discussed.

Horn, S. & Aurnou, J. M.

The Elbert Range of Magnetostrophic Convection.   I. Linear Theory

https://doi.org/10.1098/rspa.2022.0313

In magnetostrophic rotating magnetoconvection, a fluid layer heated from below and cooled from above is equidominantly influenced by the Lorentz and the Coriolis forces. Strong rotation and magnetism each act separately to suppress thermal convective instability. However, when they act in concert and are near in strength, convective onset occurs at less extreme Rayleigh numbers (Ra, thermal forcing) in the form of a stationary, large-scale, inertia-less, inviscid magnetostrophic mode. Estimates suggest that planetary interiors are in magnetostrophic balance, fostering the idea that magnetostrophic flow optimizes dynamo generation. However, it is unclear if such a mono-modal theory is realistic in turbulent geophysical settings. Donna Elbert first discovered that there is a range of Ekman (Ek, rotation) and Chandrasekhar (Ch, magnetism) numbers, in which stationary large-scale magnetostrophic and small-scale geostrophic modes coexist. We extend her work by differentiating five regimes of linear stationary rotating magnetoconvection and by deriving asymptotic solutions for the critical wavenumbers and Rayleigh numbers. Coexistence is permitted if Ek<16/(27𝜋)² and Ch≥27𝜋². The most geophysically relevant regime, the Elbert range, is bounded by the Elsasser numbers 4/3(4⁴𝜋²Ek)⅓≤𝛬≤1/2(3⁴𝜋²Ek)−⅓. Laboratory and Earth’s core predictions both exhibit stationary, oscillatory, and wall-attached multi-modality within the Elbert range.

 Horn, S., Schmid, P.J. & Aurnou, J.M.

Unravelling the large-scale circulation modes in
turbulent Rayleigh–Bénard convection

https://doi.org/10.1209/0295-5075/ac3da2

The large-scale circulation (LSC) is the most fundamental turbulent coherent flow structure in Rayleigh-Bénard convection. Further, LSCs provide the foundation upon which superstructures, the largest observable features in convective systems, are formed. In confined cylindrical geometries with diameter-to-height aspect ratios of Γ≃1, LSC dynamics are known to be governed by a quasi-two-dimensional, coupled horizontal sloshing and torsional (ST) oscillatory mode. In contrast, in Γ ≳√2 cylinders, a three-dimensional jump rope vortex (JRV) motion dominates the LSC dynamics. Here, we use dynamic mode decomposition (DMD) on direct numerical simulation data of liquid metal to show that both types of modes co-exist in Γ=1 and Γ=2 cylinders but with opposite dynamical importance. Furthermore, with this analysis, we demonstrate that ST oscillations originate from a tilted elliptical mean flow superposed with a symmetric higher-order mode, which is connected to the four rolls in the plane perpendicular to the LSC in Γ=1 tanks.
2012-2022

Publications

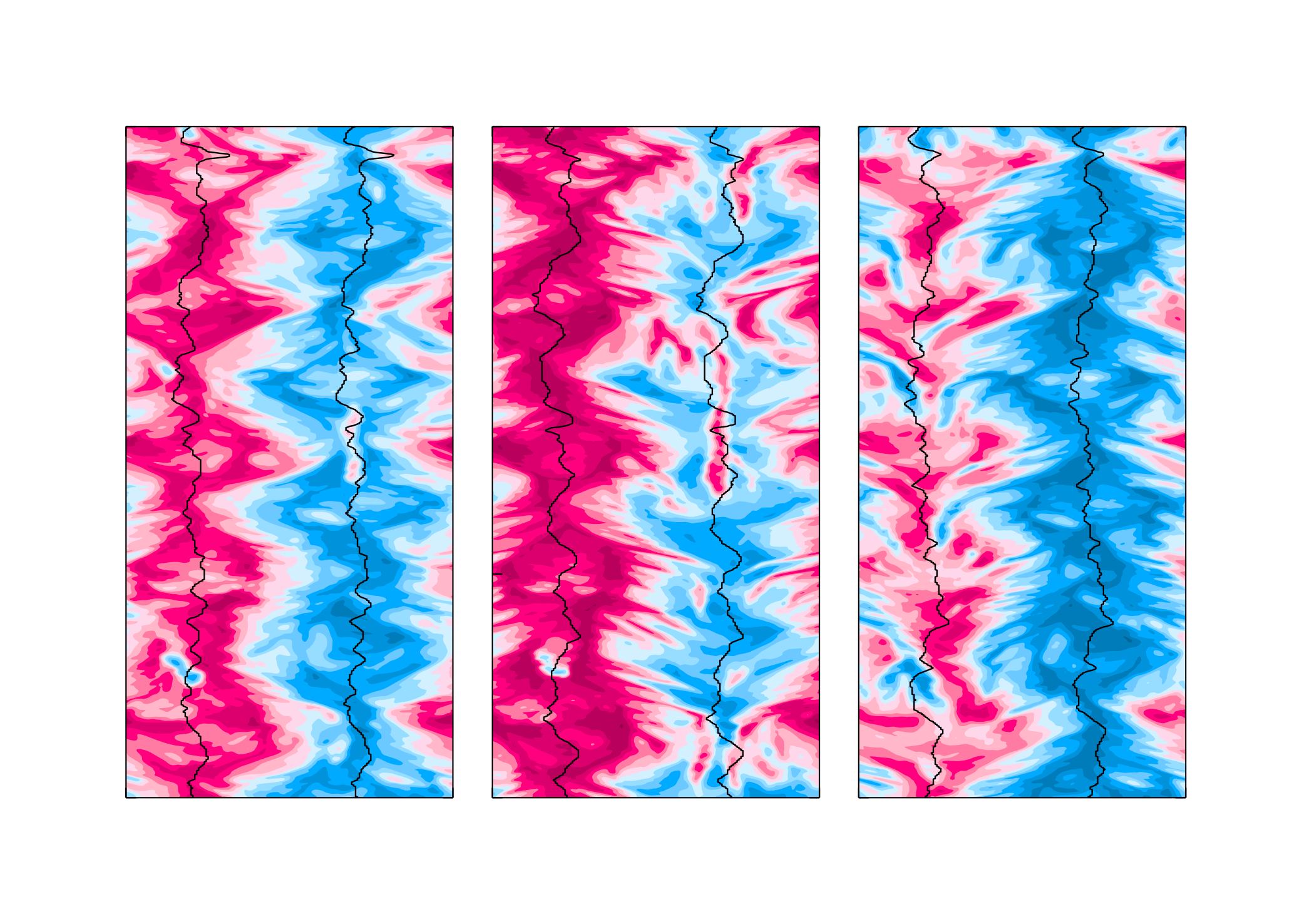
  1. Horn, S., Schmid, P.J. & Aurnou, J.M. (2022) Unravelling the large-scale circulation modes in turbulent Rayleigh–Bénard convection. Europhys. Lett. 136, 14003,  https://doi.org/10.1209/0295-5075/ac3da2                                                                                                                                                       invited article for the focus issue of EPL on “Turbulent Thermal Convection”

  2. Aggarwal, A., Aurnou, J. M. & Horn, S. (2022) Magnetic damping of jet flows in quasi-two-dimensional Rayleigh-Bénard convection. Phys. Rev. E 106, 045104, https://doi.org/10.1103/PhysRevE.106.045104

  3. Grannan, A. M., Cheng, J. S., Aggarwal, A., Hawkins, E. K., Xu, Y., Horn, S., Sánchez-Álvarez, J. & Aurnou, J. M. (2022) Experimental pub crawl from Rayleigh–Bénard to magnetostrophic convection. J. Fluid Mech. 939, R1, https://www.doi.org/10.1017/jfm.2022.204
    featured in Focus on Fluids (JFM), written by Jörg Schumacher, https://doi.org/10.1017/jfm.2022.455

  4. Akashi, M., Yanagisawa, T., Sakuraba, A., Schindler, F., Horn, S., Vogt, T. & Eckert, S. (2022) Jump rope vortex flow in liquid metal Rayleigh–Bénard convection in a cuboid container of aspect ratio five. J. Fluid Mech. 932, A27, https://doi.org/10.1017/jfm.2021.996

  5. Xu, Y., Horn, S. & Aurnou, J. M. (2022) Thermoelectric precession in turbulent magnetoconvection. J. Fluid Mech. 930, A8, https://doi.org/10.1017/jfm.2021.880 

  6. Horn, S. & Aurnou, J.M. (2021) Tornado-like vortices in the quasi-cyclostrophic regime of Coriolis-centrifugal convection. J. Turbul. 22 (4-5), 297–324, https://doi.org/10.1080/14685248.2021.1898624

  7. Vogt, T., Horn, S. & Aurnou, J.M. (2021) Oscillatory thermal–inertial flows in liquid metal rotating convection. J. Fluid Mech. 911, A5, https://doi.org/10.1017/jfm.2020.976

  8. Aurnou, J. M., Horn, S. & Julien, K. (2020) Connections between non-rotating, slowly rotating, and rapidly rotating turbulent convection transport scalings. Phys. Rev. Res. 2, 043115, https://doi.org/10.1103/PhysRevResearch.2.043115

  9. Zhang, X., van Gils, D.P.M., Horn, S., Wedi, M., Zwirner, L., Ahlers, G., Ecke, R.E., Weiss, S., Bodenschatz, E. & Shishkina, O. (2020) Boundary Zonal Flow in Rotating Turbulent Rayleigh-Bénard Convection. Phys. Rev. Lett. 124 (8), 084505, https://doi.org/10.1103/PhysRevLett.124.084505

  10. Horn, S. & Aurnou, J.M. (2019) Rotating convection with centrifugal buoyancy: Numerical predictions for laboratory experiments. Phys. Rev. Fluids 4, 073501, https://doi.org/10.1103/PhysRevFluids.4.073501

  11. Vogt, T., Horn, S., Grannan, A.M. & Aurnou, J.M. (2018) Jump Rope Vortex in Liquid Metal Convection. Proc. Natl. Acad. Sci. 115, 12674–12679, https://doi.org/10.1073/pnas.1812260115, co-first authorship

  12. Horn, S. & Aurnou, J.M. (2018) Regimes of Coriolis-Centrifugal Convection. Phys. Rev. Lett. 120, 204502, https://doi.org/10.1103/PhysRevLett.120.204502
    featured Focus article in the German Physik Journal, written by Stephan Stellmach

  13. Aurnou, J.M., Bertin, V., Grannan, A.M., Horn, S. & Vogt, T. (2018) Rotating thermal convection in liquid gallium: Multi-modal flow absent steady columns. J. Fluid Mech. 846, 846–876, https://doi.org/10.1017/jfm.2018.292

  14. Kooij, G.L., Botchev, M.A., Frederix E.M.A., Geurts, B.J., Horn, S., Lohse, D., van der Poel, E.P., Shishkina, O., Stevens, R.J.A.M. & Verzicco, R. (2018) Comparison of computational codes for direct numerical simulations of turbulent Rayleigh-Bénard convection. Comp. & Fluids 166, 1–8, https://doi.org/10.1016/j.compfluid.2018.01.010

  15. Horn, S. & Schmid, P.J. (2017) Prograde, retrograde and oscillatory modes in rotating Rayleigh–Bénard convection. J. Fluid Mech. 831, 182–211, https://doi.org/10.1017/jfm.2017.631

  16. Shishkina, O., Horn, S., Emran, M.S. & Ching, E.S.C. (2017) Mean Temperature Profiles in Turbulent Thermal Convection. Phys. Rev. Fluids 2 (11), 113502, https://doi.org/10.1103/PhysRevFluids.2.113502

  17. Shishkina, O. & Horn, S. (2016) Thermal convection in inclined cylindrical containers. J. Fluid Mech. 790, R3, https://doi.org/10.1017/jfm.2016.55

  18. Horn, S. & Shishkina, O. (2015) Toroidal and poloidal energy in rotating Rayleigh–Bénard convection. J. Fluid Mech. 762, 232–255, https://doi.org/10.1017/jfm.2014.652

  19. Shishkina, O., Horn, S., Wagner, S. & Ching, E.S.C. (2015) Thermal Boundary Layer Equation for Turbulent Rayleigh–Bénard Convection. Phys. Rev. Lett. 114 (11), 114302, https://doi.org/10.1103/PhysRevLett.114.114302

  20. Horn, S. & Shishkina, O. (2014) Rotating non-Oberbeck–Boussinesq Rayleigh–Bénard convection in water. Phys. Fluids 26, 055111, https://doi.org/10.1063/1.4878669
    featured article on the cover of Physics of Fluids

  21. Shishkina, O., Wagner, S. & Horn, S. (2014) Influence of the angle between the wind and the isothermal surfaces on the boundary layer structures in turbulent thermal convection. Phys. Rev. E 89 (3), 033014, https://doi.org/10.1103/PhysRevE.89.033014
    selected for the Kaleidoscope of Phys. Rev. E, March 2014

  22. Shishkina, O., Horn, S. & Wagner, S. (2013) Falkner–Skan boundary layer approximation in Rayleigh–Bénard convection. J. Fluid Mech. 730, 442–463, https://doi.org/10.1017/jfm.2013.347

  23. Horn, S., Shishkina, O. & Wagner, C. (2013) On non-Oberbeck–Boussinesq effects in three- dimensional Rayleigh–Bénard convection in glycerol. J. Fluid Mech. 724, 175–202, https://doi.org/10.1017/jfm.2013.151